1. Description du système

Le fonctionnement du GPS peut se résumer en cinq étapes :

1.1 Intersection spatiale (ou trilatération)

Il est nécessaire d'avoir la position de 4 satellites au minimum. Démonstration :

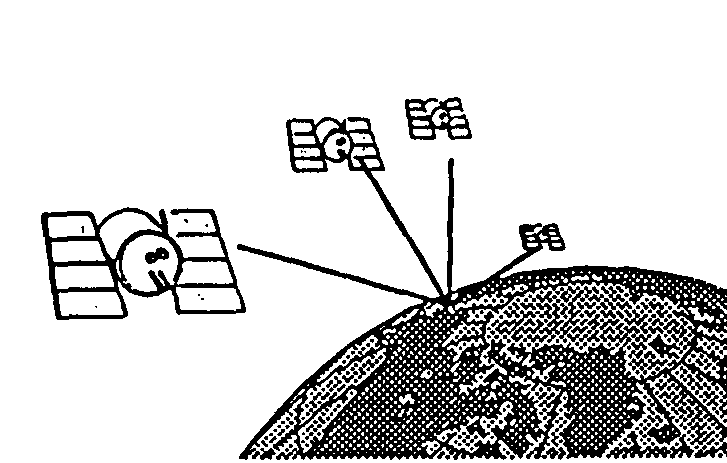
Le signal se propage à la vitesse de la lumière :

Distance = (Temps de trajet) x (Vitesse de la lumière)

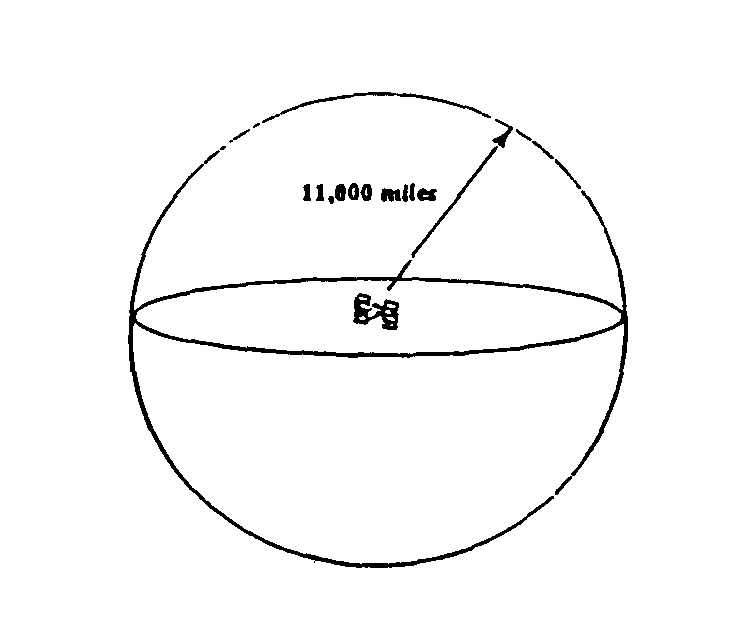
1. Le lieu géométrique (représentation) d'une mesure de distance sur un satellite est une sphère

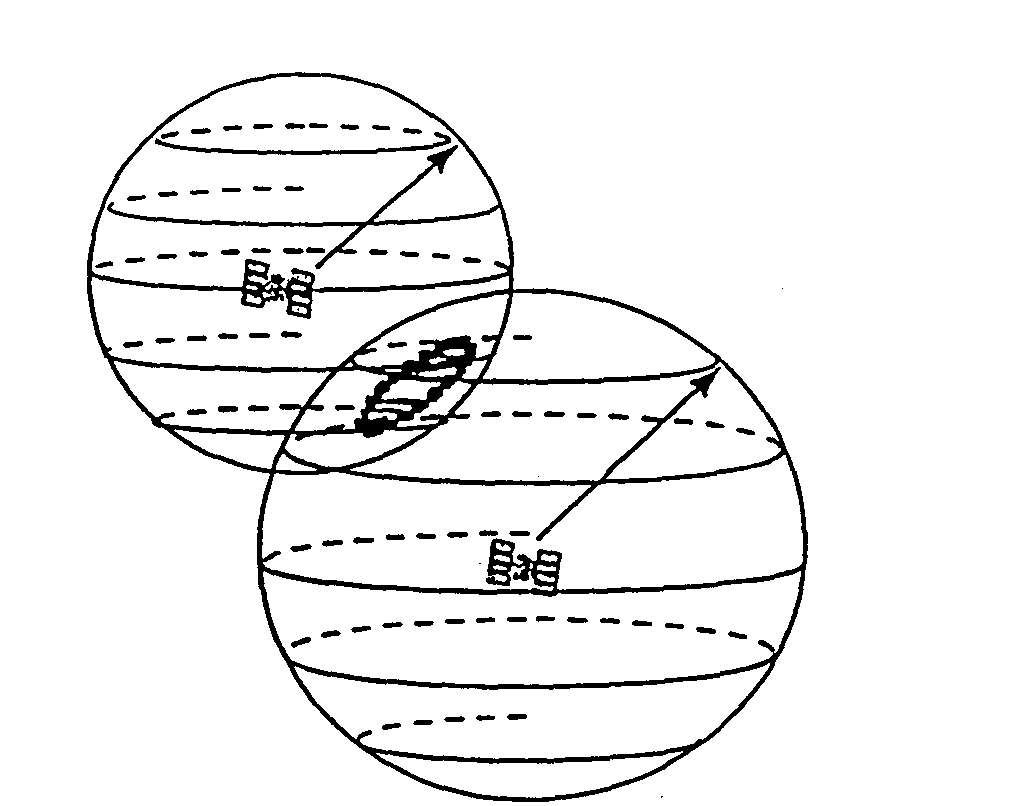
2. L'intersection de deux sphères (donc 2 satellites) est un cercle

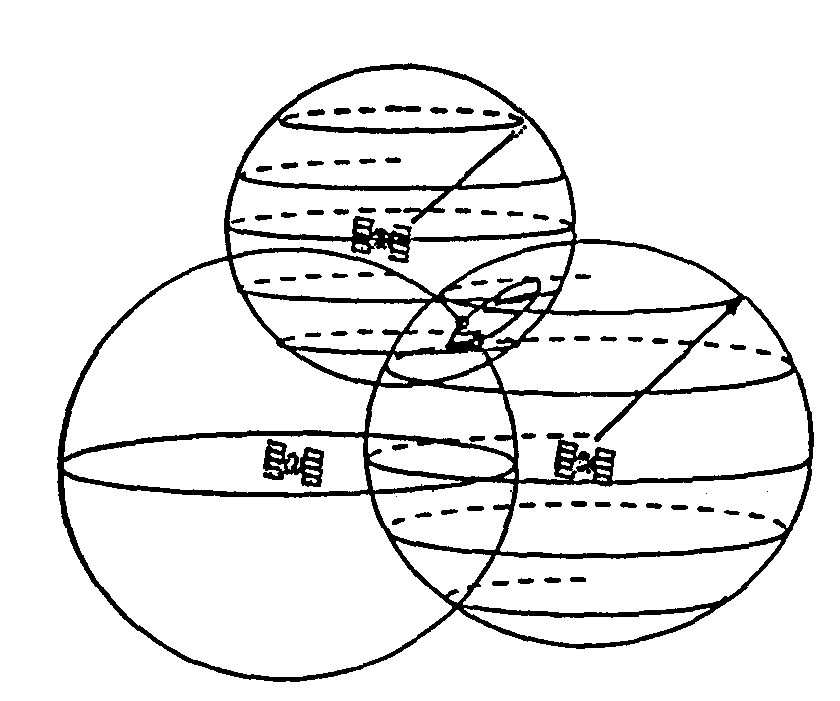
3. L'intersection de trois sphères (donc 3 satellites) est deux points dont une position est invraisemblable

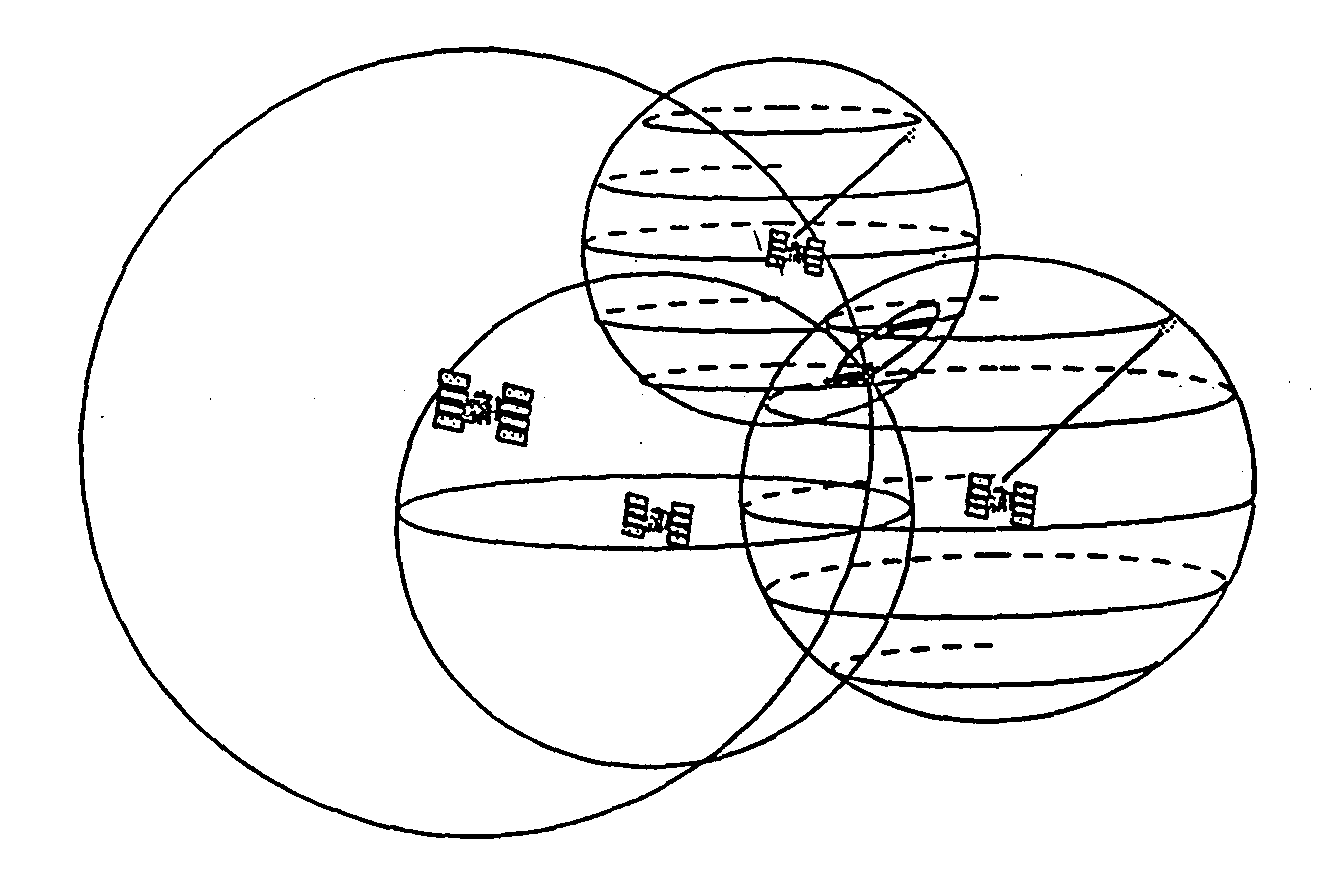
4. En pratique, un quatrième satellite est nécessaire pour résoudre les quatre inconnues, X, Y, Z et le temps

1.2 Mesure de la distance

Il y a 2 types de mesures de la distance:

1.2.1 Mesures réalisées sur le code

La distance récepteur-satellite est obtenue par la mesure du temps de trajet effectué par le signal radio : D (distance) = c (vitesse de la lumière) x T (temps).

Si l'horloge du récepteur est précise, le seul élément qui reste à connaître c'est le moment ou le signal a été émis. Comment déterminer cet instant ?

C'est une des subtilités du système GPS :

1. Chaque satellite génère son propre code sur une même fréquence commune à tous les satellites.
2. Après avoir repéré un satellite, le récepteur génère sur chaque canal le code du satellite observé.
3. Le récepteur synchronise le code qu'il génére et le code émis par le satellite.
4. Le récepteur mesure ensuite le déphasage entre le signal émis par le satellite et le signal généré dans le récepteur.

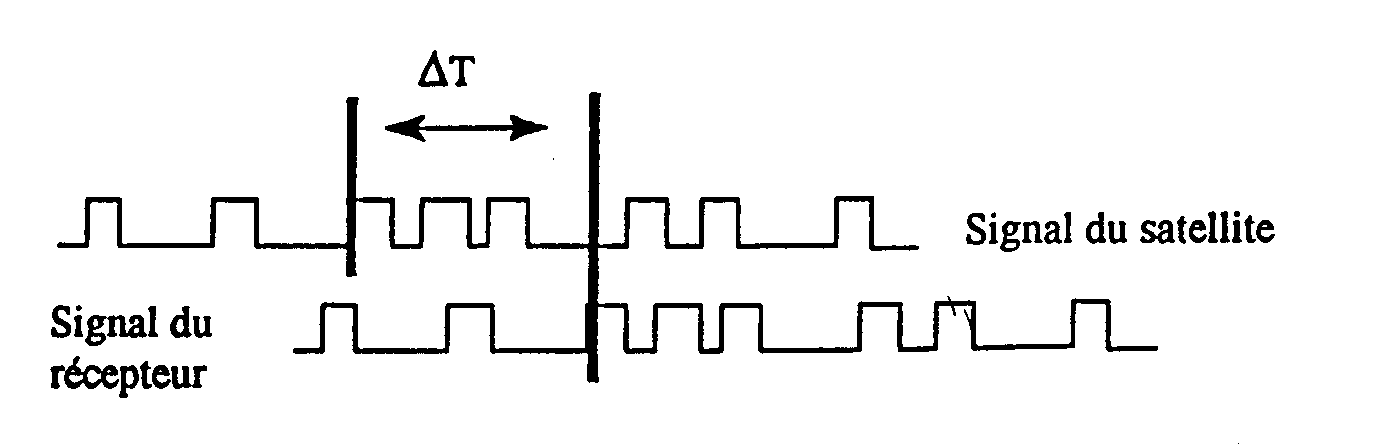
Le décalage T doit permettre au récepteur de connaître le décalage de temps "Delta t" pour connaître l'heure d'émission du code du satellite. II est donc nécessaire d'avoir des horloges précises :

• Il faut une synchronisation parfaite entre le récepteur et les satellites.

• L'ensemble du système repose sur la précision des horloges : les satellites sont équipés d'horloges atomiques et les récepteurs ont des horloges suffisamment précises.

Les mesures sur des satellites supplémentaires permettent de corriger et d'ajuster l'horloge du récepteur.

1.2.2 Mesures réalisées sur la phase

L'aspect fondamental des mesures sur la phase réside dans l'obligation d'enregistrer les variations de la phase sur au moins deux récepteurs observant les mêmes satellites (4 au minimum). Le résultat obtenu lors du traitement (temps réel ou différé) est un vecteur tridimensionnel reliant deux stations

Le traitement utilise la technique dite de la "Différenciation" :

• La simple différence compare les données de 2 satellites avec une station ou 2 stations avec un satellite.
• La double différence combine les simples différences.
• La triple différence combine les doubles différences.

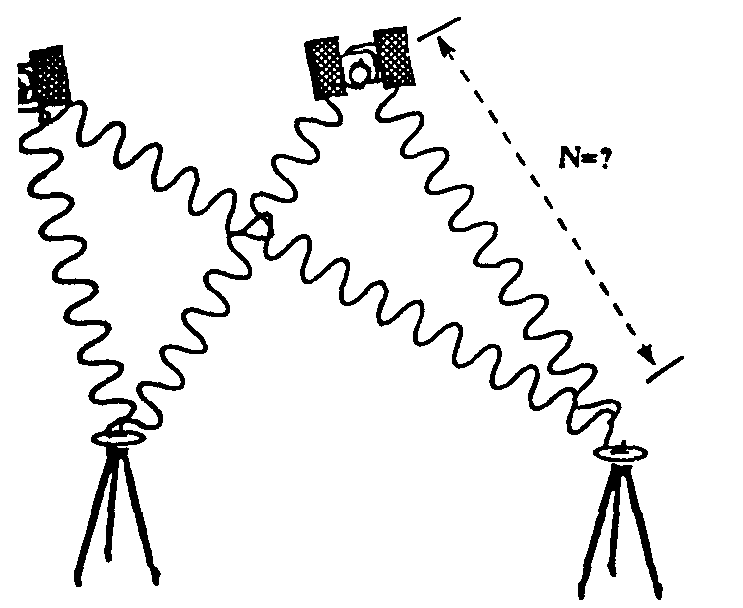
• Le récepteur mesure le déphasage lors du premier enregistrement.
• Ensuite, il comptabilise les cycles successifs
• Le nombre de longueur d'onde entière depuis la première mesure entre le récepteur et le satellite s'appelle l'ambiguïté de phase ou entier de phase.

1. Estimation des positions des récepteurs par les mesures sur le code.

2. Calcul des triples différences à partir de l'estimation précédente et de l'analyse de l'effet Doppler pour déduire une solution de la forme dX, dY, dZ, solution triple différence.

3. Détermination des ambiguïtés de phase par l'équation "dX, dY, dZ = (NA) + DeltaPhi". A ce stade les ambiguïtés sont des valeurs réelles. Ce jeu d'ambiguïtés est comparé de nouveau pour l'ensemble des données pour extraire un nouveau vecteur appelé solution flottante.

4. Les ambiguïtés sont alors arrondies à des valeurs entières les plus proches. L'ensemble des données est alors retraité avec ce jeu d'entiers. La solution obtenue est appelée solution fixe.

1.3 Mesure précise du temps

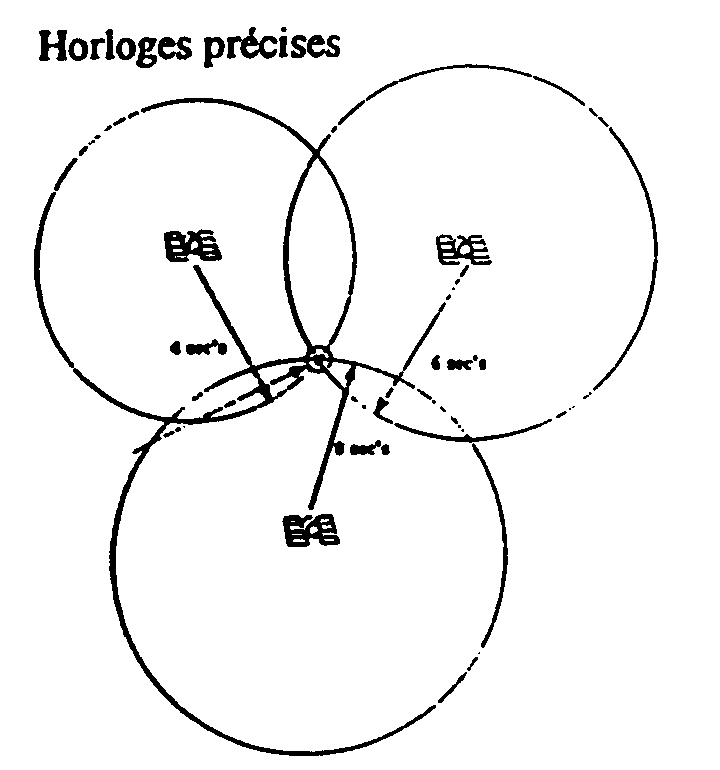
Les résultats des calculs dépendent de la précision de l'horloge. Le code doit être généré au sein du satellite et du récepteur au même instant. Les satellites ont des horloges atomiques précises à la nanoseconde (10E-9). La précision de l'horloge du récepteur est de l'ordre de la microseconde (10E-6). Le récepteur utilise en fait les mesures sur un quatrième satellite pour ajuster l'erreur de son horloge.

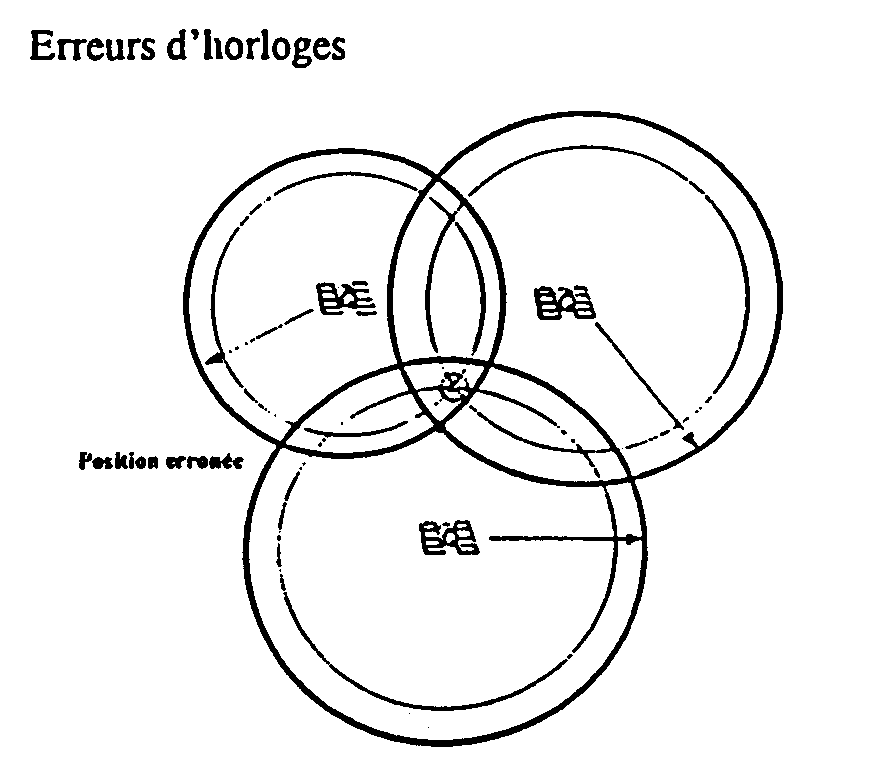
1.4 Positionnement des satellites

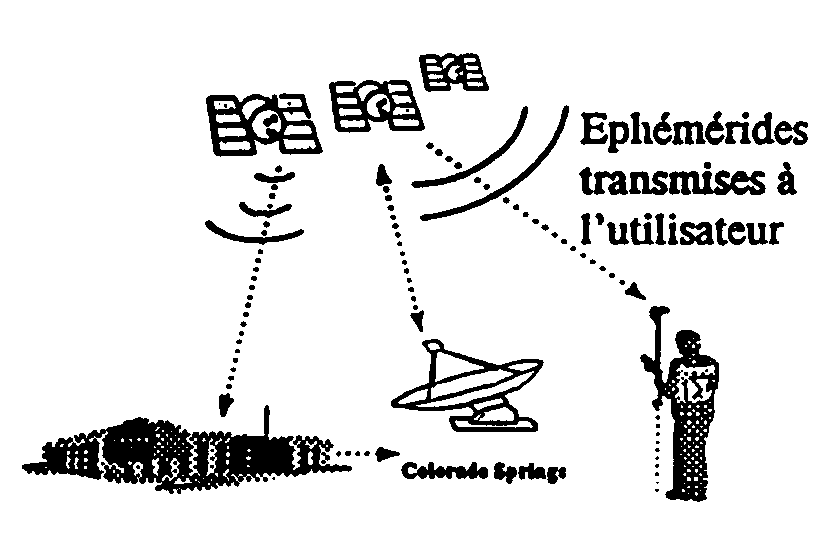
Les stations de contrôle enregistrent continuellement le signal des satellites, et transmettent ces données à la station principale de Colorado Springs qui recalcule les trajectoires et les corrections d'horloges. Ces informations sont mises à jour au niveau des satellites une fois par jour. Ces almanachs (éphémérides) sont radiodiffusés toutes les 12,5 minutes. On laisse en général se charger les éphémérides un peu avant une campagne GPS pour trouver une "fenêtre" où les erreurs sont plus faibles.

1.5 Correction des erreurs atmosphériques

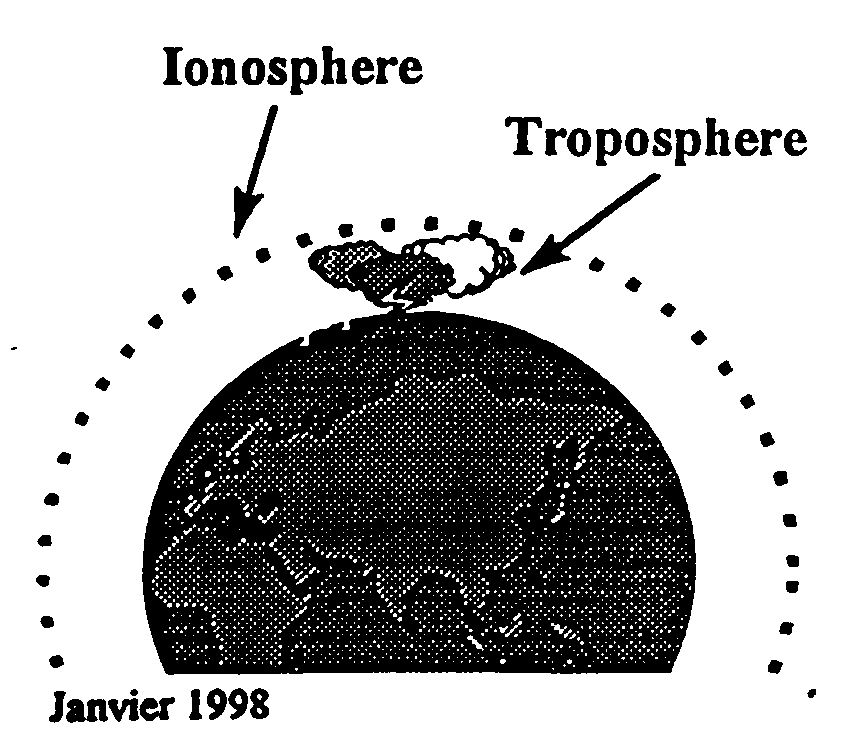
Le signal radio est retardé lors de la traversée de l'ionosphère et de la troposphère provoquant ainsi une erreur sur la mesure de distance.

Le récepteur réalise une estimation de ces retards afin de corriger cette erreur.